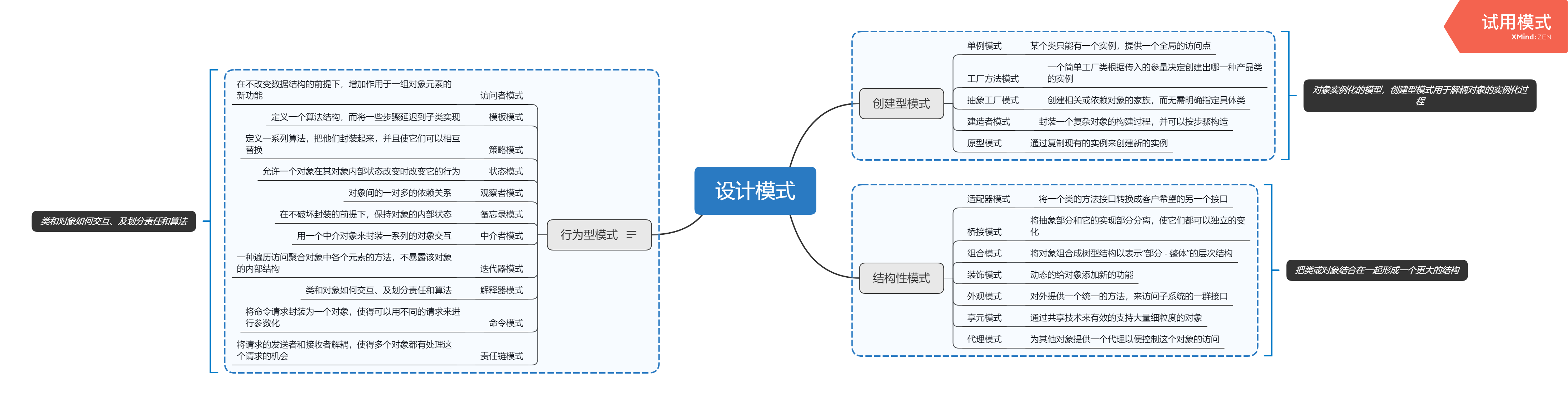
什么是设计模式?
设计模式(Design pattern)是一套被反复使用、多数人知晓的、经过分类编目的、代码设计经验的总结。使用设计模式是为了可重用代码、让代码更容易被他人理解、保证代码可靠性。 毫无疑问,设计模式于己于他人于系统都是多赢的,设计模式使代码编制真正工程化,设计模式是软件工程的基石,如同大厦的一块块砖石一样。项目中合理的运用设计模式可以完美的解决很多问题,每种模式在现在中都有相应的原理来与之对应,每一个模式描述了一个在我们周围不断重复发生的问题,以及该问题的核心解决方案,这也是它能被广泛应用的原因。简单说:
模式:在某些场景下,针对某类问题的某种通用的解决方案。
场景:项目所在的环境
问题:约束条件,项目目标等
解决方案:通用、可复用的设计,解决约束达到目标。
设计模式的三个分类
创建型模式:对象实例化的模式,创建型模式用于解耦对象的实例化过程。
结构型模式:把类或对象结合在一起形成一个更大的结构。
行为型模式:类和对象如何交互,及划分责任和算法。
设计模式.png
概说 23 种设计模式
单例模式
单例模式,它的定义就是确保某一个类只有一个实例,并且提供一个全局访问点。
单例模式具备典型的 3 个特点:
- 只有一个实例。
- 自我实例化。
- 提供全局访问点。
因此当系统中只需要一个实例对象或者系统中只允许一个公共访问点,除了这个公共访问点外,不能通过其他访问点访问该实例时,可以使用单例模式。
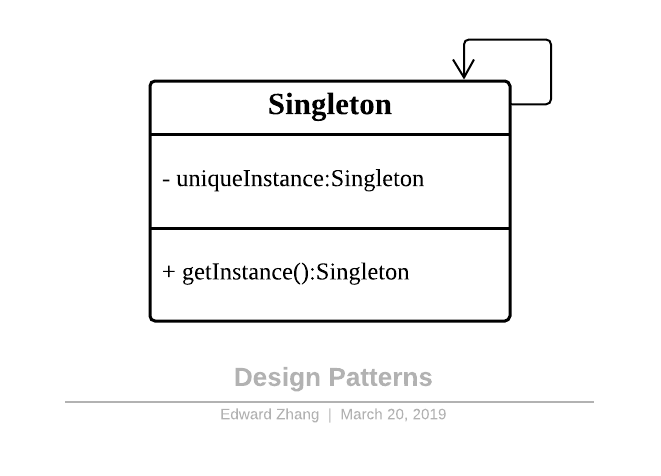
单例模式的主要优点就是节约系统资源、提高了系统效率,同时也能够严格控制客户对它的访问。也许就是因为系统中只有一个实例,这样就导致了单例类的职责过重,违背了 “单一职责原则”,同时也没有抽象类,所以扩展起来有一定的困难。其 UML 结构图非常简单,就只有一个类,如下图:
Design Patterns - Singleton.png
工厂方法模式
作为抽象工厂模式的孪生兄弟,工厂方法模式定义了一个创建对象的接口,但由子类决定要实例化的类是哪一个,也就是说工厂方法模式让实例化推迟到子类。
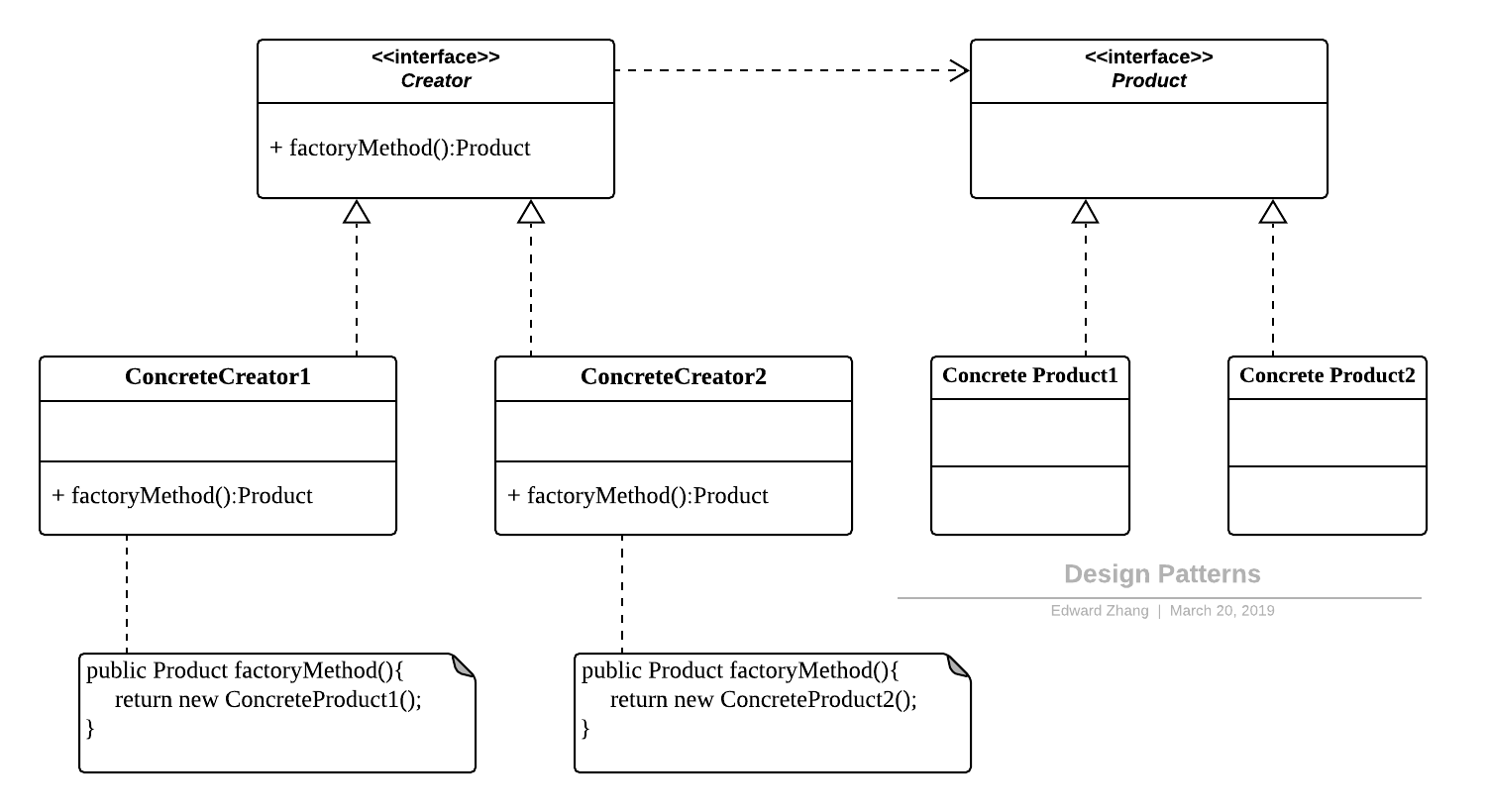
工厂方法模式非常符合“开闭原则”,当需要增加一个新的产品时,我们只需要增加一个具体的产品类和与之对应的具体工厂即可,无需修改原有系统。同时在工厂方法模式中用户只需要知道生产产品的具体工厂即可,无需关系产品的创建过程,甚至连具体的产品类名称都不需要知道。虽然他很好的符合了“开闭原则”,但是由于每新增一个新产品就需要增加两个类,这样势必会导致系统的复杂度增加。其 UML 结构图:
Design Patterns - Factory.png
抽象工厂模式
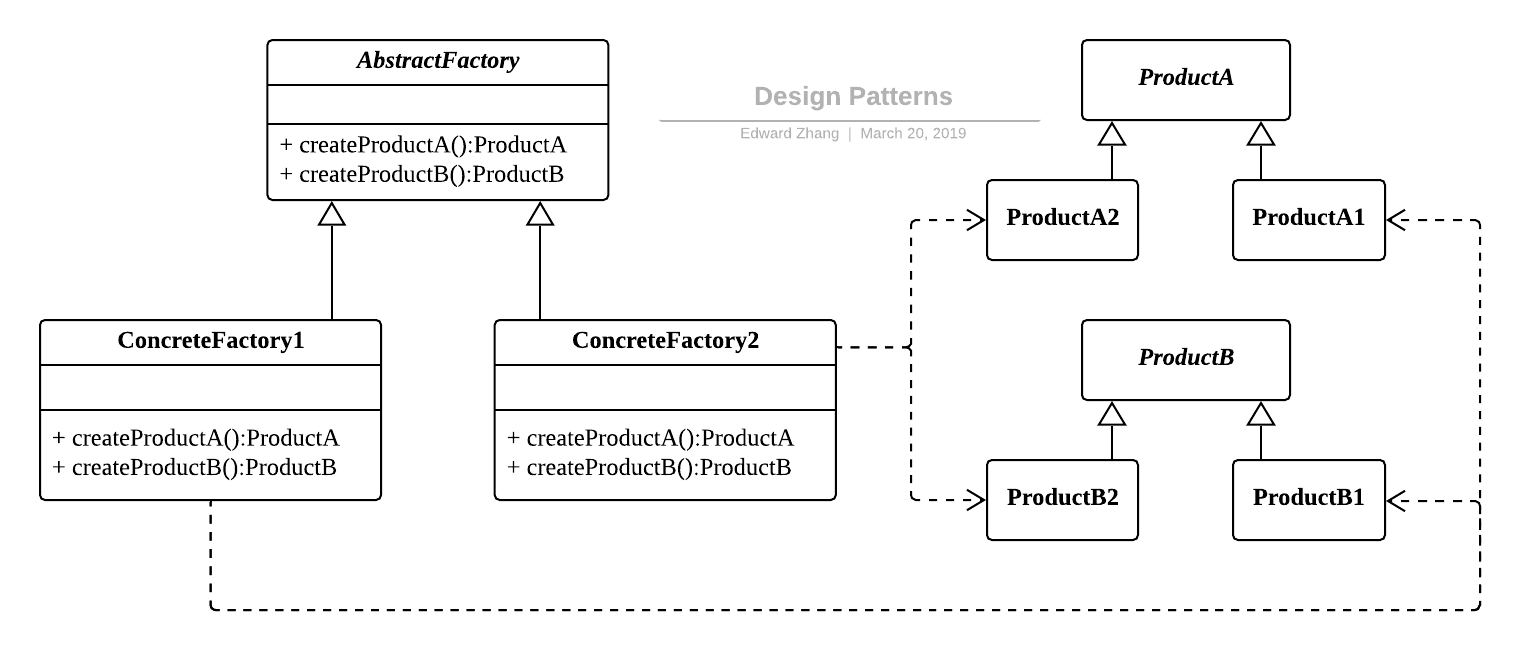
所谓抽象工厂模式就是提供一个接口,用于创建相关或者依赖对象的家族,而不需要明确指定具体类。它允许客户端使用抽象的接口来创建一组相关的产品,而不需要关系实际产出的具体产品是什么。这样一来,客户就可以从具体的产品中被解耦。它的优点是隔离了具体类的生成,使得客户端不需要知道什么被创建了,而缺点就在于新增新的行为会比较麻烦,因为当添加一个新的产品对象时,需要更改接口及其下所有子类。其 UML 结构图如下:
Design Patterns - AbstractFactory.png
建造者模式
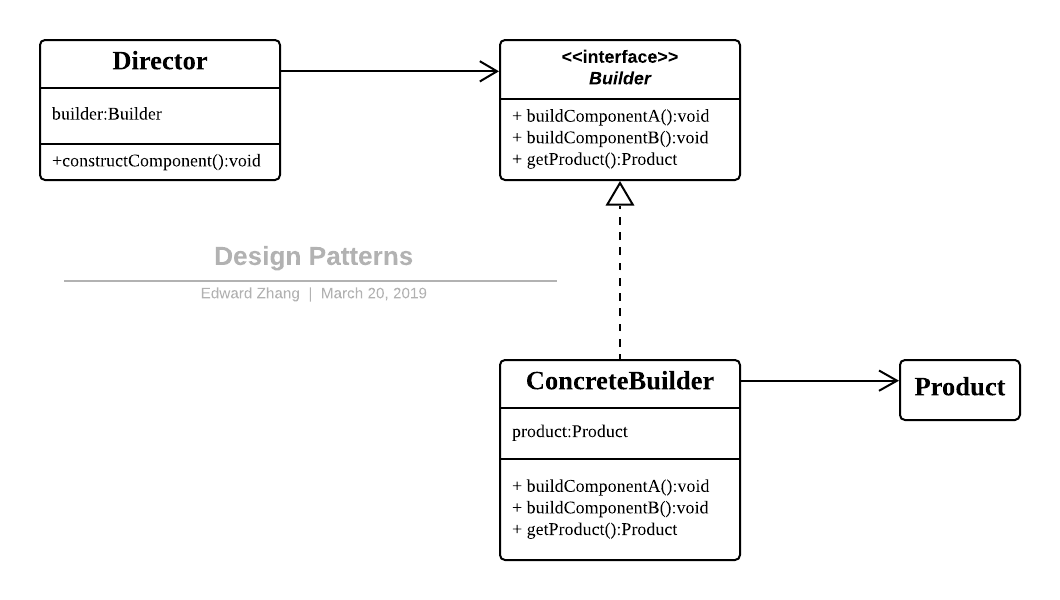
对于建造者模式,它主要是将一个复杂对象的构建与表示分离,使得同样的构建过程可以创建不同的表示。适用于那些产品对象的内部结构比较复杂。
建造者模式将复杂产品的构建过程封装分解在不同的方法中,使得创建过程非常清晰,能够让我们更加精确的控制复杂产品对象的创建过程,同时它隔离了复杂产品对象的创建和使用,使得相同的创建过程能够创建不同的产品。但是如果某个产品的内部结构过于复杂,将会导致整个系统变得非常庞大,不利于控制,同时若几个产品之间存在较大的差异,则不适用建造者模式,毕竟这个世界上存在相同点多的两个产品不是很多,所以它的使用范围有限。其 UML 结构图:
Design Patterns - Builder.png
原型模式
在我们应用程序可能有某些对象的结构比较复杂,但是我们有需要频繁的使用它们,如果这个时候我们来不断的新建这个对象势必会大大损耗系统内存的,这个时候我们需要使用原型模式来对这个结构复杂又要频繁使用的对象进行克隆。所以原型模式就是用原型实例指定创建对象的种类,并且通过复制这些原型创建新的对象。
它主要应用于那些创建新对象的成本过大时。它的主要优点就是简化了新对象的创建过程,提高了效率,同时原型模式提供了简化的创建结构。UML 结构图:
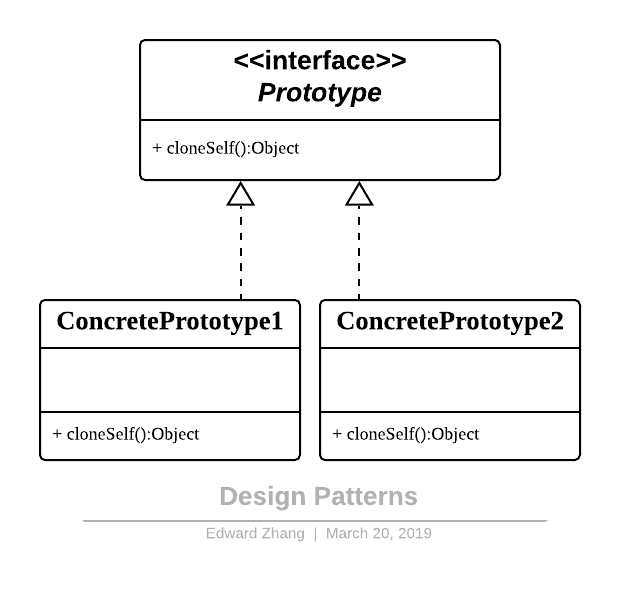
Design Patterns - Prototype.png
模式结构
原型模式包含如下角色:
Prototype:抽象原型类
ConcretePrototype:具体原型类
Client:客户类
适配器模式
在我们的应用程序中我们可能需要将两个不同接口的类来进行通信,在不修改这两个的前提下我们可能会需要某个中间件来完成这个衔接的过程。这个中间件就是适配器。所谓适配器模式就是将一个类的接口,转换成客户期望的另一个接口。它可以让原本两个不兼容的接口能够无缝完成对接。
作为中间件的适配器将目标类和适配者解耦,增加了类的透明性和可复用性。
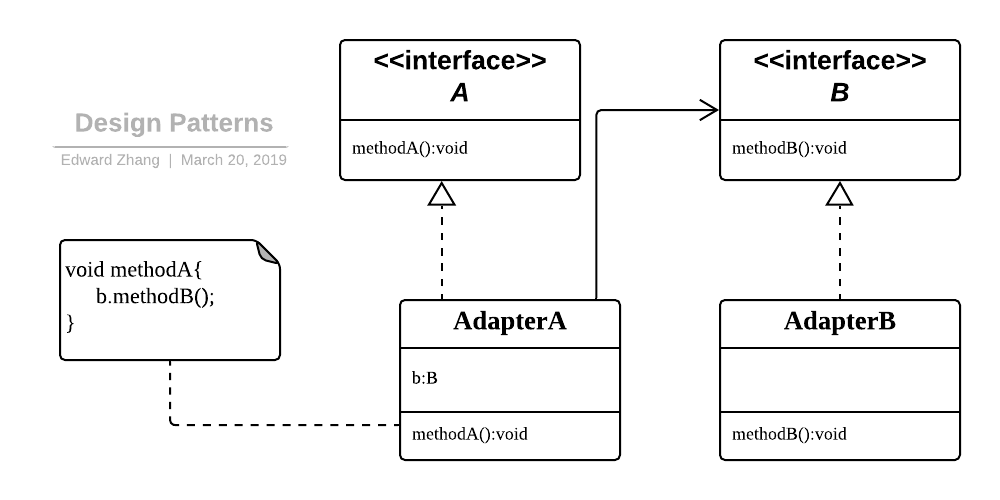
Design Patterns - Adapter.png
适配器模式包含如下角色:
Target:目标抽象类
Adapter:适配器类
Adaptee:适配者类
Client:客户类
桥接模式
别名:柄体模式
- 将抽象部分与它的实现部分分离,使它们都可以独立地变化。
如果说某个系统能够从多个角度来进行分类,且每一种分类都可能会变化,那么我们需要做的就是讲这多个角度分离出来,使得他们能独立变化,减少他们之间的耦合,这个分离过程就使用了桥接模式。所谓桥接模式就是讲抽象部分和实现部分隔离开来,使得他们能够独立变化。
桥接模式将继承关系转化成关联关系,封装了变化,完成了解耦,减少了系统中类的数量,也减少了代码量。
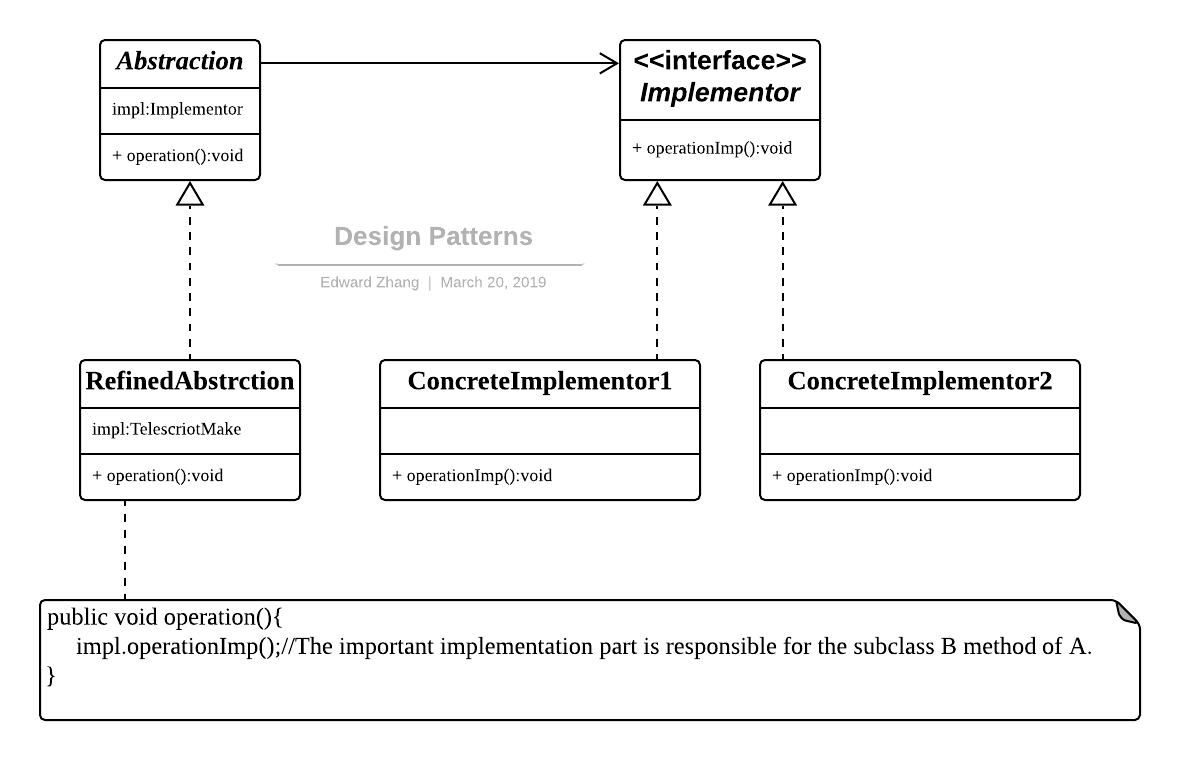
Design Patterns - Handle-Body.png
桥接模式包括如下角色:
- 抽象(Abstraction):是一个抽象类,该抽象类含有 Implementor 声明的变量,即维护一个 Implementor 类型对象。
- 实现者(Implementor):实现者角色是一个接口(抽象类),该接口(抽象类)中的方法不一定与 Abstraction 类中的方法一致。Implementor 接口(抽象类)负责定义基本操作,而 Abstraction 类负责定义基于操作的较高层次的操作。
- 细化抽象(Refined Abstraction):细化抽象是抽象角色的一个子类,该子类在重写(覆盖)抽象角色中的抽象方法时,在给出一些必要的操作后,将委托所维护 Implementor 类型对象调用相应的方法。
- 具体实现者(Concrete Implementor):具体实现者是实现(扩展)Implementor 接口(抽象类)的类。
未完待续。。。
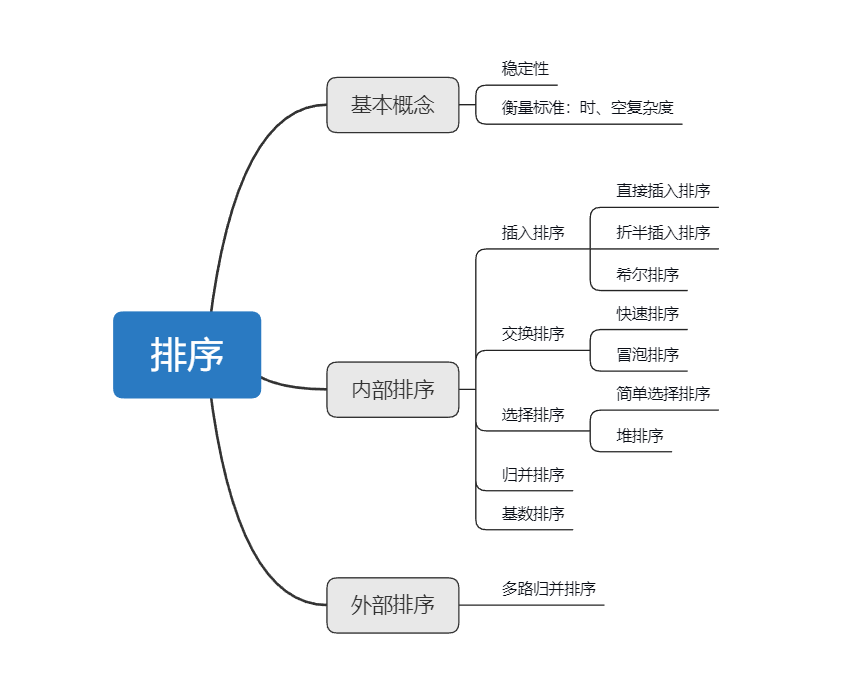
排序算法
插入排序
直接插入排序
| 时间复杂度 |
空间复杂度 |
稳定性 |
| $O(n^2)$ |
$O(1)$ |
√ |
1 2 3 4 5 6 7 8 9 10 11 12 13 14
| public static void insertSort(int[] array){ for(int i=1;i<array.length;i++){ if(array[i]<array[i-1])({ int temp=array[i]; int k = i - 1; for(int j=k;j>=0 && temp<array[j];j--){ array[j+1]=array[j]; k--; } array[k+1]=temp; } } }
|
折半插入排序
| 时间复杂度 |
空间复杂度 |
稳定性 |
| $O(n^2)$ |
$O(1)$ |
√ |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
| private static void binaryInsertSort(int[] array) { for (int i = 1; i < array.length; i++) { int temp = array[i]; int low = 0; int high = i - 1; while (low <= high) { int mid = (low + high) / 2; if (temp < array[mid]) { high = mid - 1; } else { low = mid + 1; } } for (int j = i; j >= low + 1; j--) { array[j] = array[j - 1]; } array[low] = temp; } }
|
Shell 排序
| 时间复杂度 |
空间复杂度 |
稳定性 |
| $O(n^{1.3})$ ~ $O(n^2)$ |
$O(1)$ |
× |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
| * 希尔排序的原理:根据需求,如果你想要结果从小到大排列,它会首先将数组进行分组,然后将较小值移到前面,较大值 * 移到后面,最后将整个数组进行插入排序,这样比起一开始就用插入排序减少了数据交换和移动的次数, * 可以说希尔排序是加强 版的插入排序 拿数组5, 2,8, 9, 1, 3,4来说,数组长度为7,当increment为3时,数组分为两个序列 * 5,2,8和9,1,3,4,第一次排序,9和5比较,1和2比较,3和8比较,4和比其下标值小increment的数组值相比较 * 此例子是按照从小到大排列,所以小的会排在前面,第一次排序后数组为5, 1, 3, 4, 2, 8,9 * 第一次后increment的值变为3/2=1,此时对数组进行插入排序, 实现数组从大到小排 */ public static void shellSort(int[] data) { int j = 0; int temp = 0; for (int increment = data.length / 2; increment > 0; increment /= 2) { for (int i = increment; i < data.length; i++) { temp = data[i]; for (j = i; j >= increment; j -= increment) { if (temp < data[j - increment]) { data[j] = data[j - increment]; } else { break; } } data[j] = temp; } } }
|
交换排序
冒泡排序
| 时间复杂度 |
空间复杂度 |
稳定性 |
| $O(n^2)$ |
$O(1)$ |
× |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
| public static void bubbleSort(int[] numbers){ int temp = 0; int size = numbers.length; boolean flag = true; for(int i = 0;i < size-1&&flag; i++){ flag = false; for(int j = 0; j < size-1-i; j++){ if(numbers[j] >numbers[j+1]){ temp = numbers[j]; numbers[j] = numbers[j + 1]; numbers[j + 1] = temp; flag = true; } } } }
|
快速排序
| 时间复杂度 |
空间复杂度 |
稳定性 |
| $O(nlogn)$ |
$O(log_2n)$ ~ $O(n)$ |
× |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56
| * 快速排序 * * @param numbers * 带排序数组 */ public static void quick(int[] numbers) { if (numbers.length > 0) { quickSort(numbers, 0, numbers.length - 1); } } * * @param numbers * 带排序数组 * @param low * 开始位置 * @param high * 结束位置 */ public static void quickSort(int[] numbers, int low, int high) { if (low >= high) { return; } int middle = getMiddle(numbers, low, high); quickSort(numbers, low, middle - 1); quickSort(numbers, middle + 1, high); } * 查找出中轴(默认是最低位low)的在numbers数组排序后所在位置 * * @param numbers * 带查找数组 * @param low * 开始位置 * @param high * 结束位置 * @return 中轴所在位置 */ public static int getMiddle(int[] numbers, int low, int high) { int temp = numbers[low]; while (low < high) { while (low < high && numbers[high] > temp) { high--; } numbers[low] = numbers[high]; while (low < high && numbers[low] < temp) { low++; } numbers[high] = numbers[low]; } numbers[low] = temp; return low; }
|
选择排序
简单选择排序
| 时间复杂度 |
空间复杂度 |
稳定性 |
| $O(n^2)$ |
$O(1)$ |
× |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
| public static void selectSort(int[] numbers) { int size = numbers.length; int temp = 0; for (int i = 0; i < size-1; i++) { int k = i; for (int j = size - 1; j > i; j--) { if (numbers[j] < numbers[k]) { k = j; } } temp = numbers[i]; numbers[i] = numbers[k]; numbers[k] = temp; } }
|
堆排序
| 时间复杂度 |
空间复杂度 |
稳定性 |
| $O(nlog_2n)$ |
$O(1)$ |
× |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
| public static void heapSort(int[] a){ int arrayLength = a.length; for (int i = 0; i < arrayLength - 1; i++) { buildMaxHeap(a, arrayLength - 1 - i); swap(a, 0, arrayLength - 1 - i); System.out.println(Arrays.toString(a)); } } public static void buildMaxHeap(int[] data, int lastIndex) { for (int i = (lastIndex - 1) / 2; i >= 0; i--) { int k = i; while (k * 2 + 1 <= lastIndex) { int biggerIndex = 2 * k + 1; if (biggerIndex < lastIndex) { if (data[biggerIndex] < data[biggerIndex + 1]) { biggerIndex++; } } if (data[k] < data[biggerIndex]) { swap(data, k, biggerIndex); k = biggerIndex; } else { break; } } } } private static void swap(int[] data, int i, int j) { int tmp = data[i]; data[i] = data[j]; data[j] = tmp; }
|
归并排序
| 时间复杂度 |
空间复杂度 |
稳定性 |
| $O(nlog_2n)$ |
$O(n)$ |
√ |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54
| * 归并排序 * 简介:将两个(或两个以上)有序表合并成一个新的有序表 即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列 * 时间复杂度为O(nlogn) * 稳定排序方式 * @param nums 待排序数组 * @return 输出有序数组 */ public static int[] sort(int[] nums, int low, int high) { int mid = (low + high) / 2; if (low < high) { sort(nums, low, mid); sort(nums, mid + 1, high); merge(nums, low, mid, high); } return nums; } * 将数组中low到high位置的数进行排序 * @param nums 待排序数组 * @param low 待排的开始位置 * @param mid 待排中间位置 * @param high 待排结束位置 */ public static void merge(int[] nums, int low, int mid, int high) { int[] temp = new int[high - low + 1]; int i = low; int j = mid + 1; int k = 0; while (i <= mid && j <= high) { if (nums[i] < nums[j]) { temp[k++] = nums[i++]; } else { temp[k++] = nums[j++]; } } while (i <= mid) { temp[k++] = nums[i++]; } while (j <= high) { temp[k++] = nums[j++]; } for (int k2 = 0; k2 < temp.length; k2++) { nums[k2 + low] = temp[k2]; } }
|
基数排序
| 时间复杂度 |
空间复杂度 |
稳定性 |
| $O(d(n+r))$ |
$O(r)$ |
√ |